Linear Regression:

Simple Linear Regression:

Allows to understand the Relationship between two Continuous Variables.

Examples:
- x : Independent Variable
  - Weight
- y : Dependent Variable
  - Height

$y = \alpha x + \beta$

Aim of Linear Regression.

Minimize the distance between the points and the line ( $y = \alpha x + \beta$ ).

Adjusting:
- Coefficient: $\alpha$
- Bias/intercept: $\beta$

Building a Linear Regression Model with PyTorch:

Example

Coefficient: \alpha = 2

Bias/intercept: \beta = 1

Equation: y = 2x + 1

Building a Toy Dataset:

# Creating a list of values from 0 to 11
x = [i for i in range(11)]

x

🤙
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

Convert list of numbers into NumPy array:

x_train = np.array(x, dtype = np.float32)

x_train.shape

🤙
(11,)

Convert into 2D array:

If you don't do this you'll get an error stating you need 2D. Simply just reshape accordingly if you ever face such errors.

x_train = x_train.reshape(-1,1)

x_train.shape

🤙
(11,1)

Create a list of y values:

We want y values for every x value we have above.

$y = 2x + 1$

y = [(2 * i + 1) for i in x]

y

🤙
[1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21]

Convert it into NumPy Array and reshape to 2D:

y_train = np.array(y,dtype= np.float32)

y_train = y_train.reshape(-1,1)

y_train.shape

🤙
(11, 1)

Building a Model PyTorch:

# Importing Libraries:
import torch
import torch.nn as nn

Create Model:

Linear model
- True Equation: $y = 2x + 1$

Forward
- Example
  - Input $x = 1$
  - Output $\hat y = ?$

class LinearRegression(nn.Module):
  def __init__(self,input_dim, output_dim):
    super(LinearRegression, self).__init__()
    self.linear = nn.Linear(input_dim, output_dim)
  
  def forward(self, x):
    out = self.linear(x)
    return out

Instantiate Model Class:

input: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

desired output: [1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21]

input_dim = 1
output_dim = 1

model = LinearRegressionModel(input_dim, output_dim)

Instantiate Loss Class:

MSE Loss: Mean Squared Error

MSE = $\frac{1}{n} \sum_{i=1}^n(\hat y_i - y_i)^2$
- $\hat y$ : prediction
- $y$ : true value

criterion = nn.MSELoss()

Instantiate Optimizer Class:

Simplified equation
- $\theta = \theta - \eta \cdot \nabla_\theta$
  - $\theta:$ parameters (our variables)
  - $\eta$ : learning rate (how fast we want to learn)
  - $\nabla_\theta$ : parameters' gradients

Even simplier equation
- parameters = parameters - learning_rate * parameters_gradients
  - parameters: $\alpha$ and $\beta$ in $y = \alpha x + \beta$
  - desired parameters: $\alpha = 2$ and $\beta = 1$ in $y = 2x + 1$

learning_rate = 0.01

optim = torch.optim.SGD(model.parameters(), lr = learning_rate)

Use GPU for the model:

device = torch.device('cuda' if torch.cuda.is_available else 'cpu')
model.to(device)

Train a Model:

1 epoch: going through the whole x_train data once

100 epochs:
- 100x mapping x_train = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

Process:
1. Convert inputs/labels into tensors with gradients.
1. Clear Gradient Buffers.
1. Get outputs from given inputs.
1. Get the Loss.
1. Get Gradients w.r.t the Parameters.
1. Update the Parameters using Gradiens.
  parameters = parameters - learning_rate * parameters_gradients
1. Repeat

epochs = 100

for epoch in range(epochs):
  epoch+=1

  # Convert numpt variable into tensor with gradients
  inputs = torch.from_numpy(x_train).to(device)
  labels = torch.from_numpy(y_train).to(device)

  # clear the gradients w.r.t Paramters.
  optim.zero_grad()

  # Forward to get output:
  output = model(inputs)

  # Calcualte the loss
  loss = criterion(output, labels)

  # Getting Gradients w.r.t Parameters.
  loss.backward()

  # Update the Parameters.
  optim.step()

  # Logging
  print('epoch {}, loss {}'.format(epoch, loss.item()))

🤙
epoch 95, loss 0.00018149390234611928
epoch 96, loss 0.0001794644631445408
epoch 97, loss 0.00017746571393217891
epoch 98, loss 0.00017548113828524947
epoch 99, loss 0.00017352371651213616
epoch 100, loss 0.00017157981346827

Looking at the Predicted Values:

# Purely inference
predicted = model(torch.from_numpy(x_train).to(device).requires_grad_())
predicted

Plot of Predicted and Actual Values:

# Clear Figure:
plt.clf()

# Plot True Data
plt.plot(x_train, y_train, 'go', label = 'True Data', alpha = 0.5)

# PLot predictions
plt.plot(x_train, predicted, '--', label = 'Predictions', alpha = 0.5)

# Legend and plot
plt.legend(loc = 'best')
plt.show()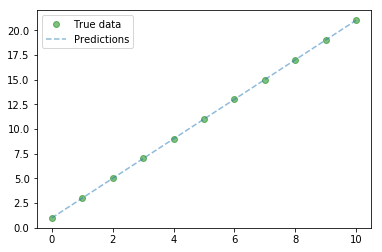

Save Model:

save_model = False
if save_model is True:
  # Saves only parameters
    # alpha & beta
    torch.save(model.state_dict(),'model.pkl')

Load Model:

load_model = False
if load_model is True:
  model.load_state_dict(torch.load('model.pkl'))

Summary:

Simple linear regression basics
- y = Ax + B
- y = 2x + 1

Example of simple linear regression

Aim of linear regression

Minimizing distance between the points and the line
- Calculate "distance" through MSE
- Calculate gradients
- Update parameters with parameters = parameters - learning_rate * gradients
- Slowly update parameters A and B model the linear relationship between y and x of the form y = 2x + 1

Built a linear regression model in CPU and GPU
- Step 1: Create Model Class
- Step 2: Instantiate Model Class
- Step 3: Instantiate Loss Class
- Step 4: Instantiate Optimizer Class
- Step 5: Train Model

Important things to be on GPU
- model
- tensors with gradients

How to bring to GPU?
- model_name.to(device)
- variable_name.to(device

Reference:

[Notebook Link]